7 Conclusions
This chapter concludes the thesis by discussing its most important contributions, some promising avenues for future work, and broader reflections about the work.
7.1 Contributions
Effective response to the HIV epidemic depends on strategic information provided by models of data. This thesis contributes both to generating this information and to advancing statistical methods.
Chapter 4 found that spatially structured random effects should be used in small-area models for HIV. Kernel models performed better for data simulated from an adjacency-based spatial process than adjacency-based models did for data simulated from a kernel model. However, adjacency-based models performed better under cross-validation of real HIV survey data. Model comparison was conducted using strictly proper scoring rules, with checks for calibration.

Figure 7.1: Panel A shows the front page of UNAIDS (2023b). Panel B shows the page containing text and a figure based on the work done in Chapter 5. In this figure, 30 countries are included.
Chapter 5 estimated HIV risk group proportions for AGYW to enable implementation of the Global AIDS strategy (UNAIDS 2021b).
Risk group proportion estimates were used to behaviourally disaggregate HIV prevalence and incidence and assess the benefits of a variety of risk stratification strategies.
This work is the basis for a tool used to prioritise delivery of HIV prevention services by countries in SSA.
The tool now encompasses at least 30 countries, expanding from the initial 13 included [Figure 7.1; UNAIDS (2023b)].
Models will be rerun each year to populate the tool with updated information as a part of the UNAIDS annual HIV estimates process.
Alongside these applied contributions, Chapter 5 exemplified specification of complex multinomial spatio-temporal models in R-INLA using the Poisson-multinomial transformation, including using two- and three-way Kronecker product interactions.
The Naomi model has been used in over 35 countries in SSA to produce district-level estimates of HIV indicators by synthesising evidence from multiple sources.
Chapter 6 developed deterministic Bayesian inference methods, motivated by the aim of providing more accurate inferences for this challenging and practically important model.
Its most important methodological contributions are two-fold.
First, an implementation of INLA which is compatible with models specified using a TMB C++ template.
For the first time, practitioners can now fit essentially any model using the INLA method.
Second, a quadrature rule which combines PCA and AGHQ to naturally extend the applicability of INLA methods to moderate hyperparameter dimension, allowing more complex models to be fit.
Additionally, Chapter 6 provides detailed description and analysis of the Naomi model.
Indeed, Esra et al. (2024) used tables and text from Appendix C in an update to Eaton et al. (2021).
7.2 Future work
Promising avenues for future work, that I might prioritise, include:
It would be valuable to extend the risk group model developed in Chapter 5, and the resulting tool, to include all adults 15-49. Although AGYW are disproportionately at risk of HIV infection, 56% of new infections in SSA occur in other demographic groups. Modelling of age-stratified sexual partnerships (Wolock et al. 2021) may help to overcome reporting biases by harmonising male and female reporting. This model would likely fall outside the scope of
R-INLA, but would be possible to write withTMBand therefore amenable to the inference methods advanced in Chapter 6.Although suitable for early stage research, wider adoption of the INLA implementation developed in Chapter 6 would be greatly enhanced by improvements to its speed and usability. The most important speed enhancement would come from using the simplified approximation to the Laplace marginals developed by Wood (2020). Although the naive implementation used in this thesis is viable for integrating Laplace marginals over a small number of hyperparameter quadrature nodes, such as the \(3^2 = 9\) nodes used Sections 6.2.2 and 6.2.1, it becomes prohibitively slow for larger numbers. Usability would be improved by providing the method as a part of statistical software, likely via the
aghqpackage. The primary difficulty which would have to be overcome to do so is that therandomargument ofTMB::MakeADFundoes not allow indexing.
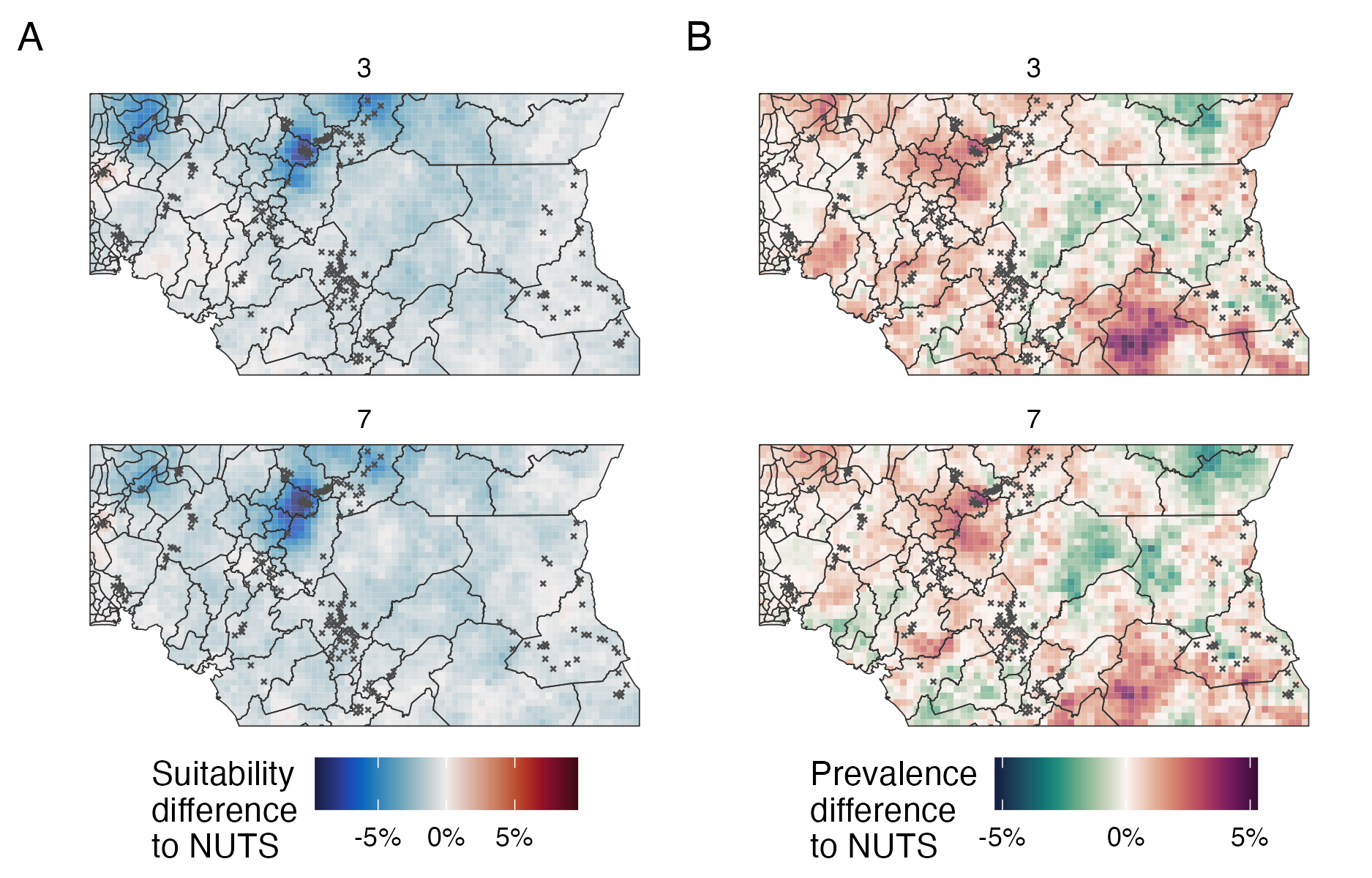
Figure 7.2: For the Loa loa ELGM (Section 6.2.2), increasing the number of quadrature nodes per hyperparameter dimension from \(k = 3\) to \(k = 7\) did little to improve accuracy. On the other hand, using Laplace marginals rather than Gaussian marginals did have a substantial effect (Figures 6.12 and 6.13). It would be valuable to better understand, and aspirationally have diagnostics for, the circumstances under which accuracy of INLA methods could be improved by additional computation.
The universal INLA implementation developed in Chapter 6 enables empirical and methodological research that was previously not possible, or prohibitively difficult.
INLA-like methods can now be tested for a broader class of models, such as the Loa loa and Naomi ELGMs (Sections 6.2.2 and 6.5). That a single
TMBC++ template for the log-posterior supports inference using multiple methods, including gold-standard NUTS viatmbstan, is a substantial asset in conducting this type of research.As an example research question, within this class of models, what is the best way to obtain accurate inferences within a fixed computational budget. Is it better to use additional hyperparameter grid points, or more accurate latent field approximations? For the Loa loa ELGM in Section 6.2.2, the benefit of using Laplace marginals exceeded that of a denser AGHQ grid (Figure 7.2). It would also be of interest to find methods to obtain accurate inferences for particular parameters, or functions of parameters, using INLA-like methods. For example, in Section 6.5, although the PCA-AGHQ grid improved latent field parameter inferences, it did little to improve model output accuracy. Is there a way in which computational effort could be focused on obtaining accurate estimates of Naomi model outputs?
Additionally, it is relatively easy to make alterations to the implementation, facilitating possible innovation in the design of INLA-like algorithms. Previously, it has been difficult for researchers not involved in development of
R-INLAto engage in methodological work about the INLA method.Theoretical research could be conducted to complement the work described above, extending the findings of Bilodeau, Stringer, and Tang (2022). This work is benefited by the complete specification (Appendix C.3) of the INLA-like algorithm used in this thesis.
7.3 Broader reflections
Conducting the work in this thesis involved testing the boundaries of available statistical software.
For example, I found it challenging, if not impossible, to implement a common model using different inferential software.
As the Frequently Asked Questions section of the R-INLA website (Havard Rue 2023) notes: “the devil is in the details”.
Similarly, I encountered issues implementing a desired collection of different models in a common inferential software.
From personal experience, my colleagues have also encountered similar problems.
Needless to say, conflation of statistical models and inference methodologies limits the validity of any findings.
To avoid this issue I implemented all models in Chapters 4 and 6 using TMB model templates.
(Additionally, I would recommend implementing the model used in Chapter 5 in TMB for future development.)
Alongside being sufficiently flexible to meet my model specification requirements, TMB is compatible with a range of inference methodologies, including those advanced in this thesis.
As such, TMB remains (Osgood-Zimmerman and Wakefield 2023) an under-rated statistical tool.
In demonstrating some of its capabilities, I hope this thesis contributes to its wider adoption.
The work done in this thesis, particularly Chapters 4 and 6, focused on producing experimental, empirical evidence. This approach reflects the complexity of the models and methods used in this thesis. Understanding complex systems from a theoretical perspective can be challenging. That said, in my opinion the work in this thesis could benefit from closer integration with statistical theory. Although a full theoretical understanding of these models or algorithms may be ambitious, better understanding simplified examples, limiting cases, or constituent parts could still prove valuable.
Working with the data in Chapter 5 deepened my appreciation for the realistic challenges faced in applied work, and data quality being linchpin for any successful statistical analysis. While from the real world, the data in Chapters 4 and 6 underwent substantial cleaning, processing, and vetting before I handled them, as is typical in methodological research. It is important that methodological and theoretical statisticians appreciate the real challenges of applied work, by doing it themselves, or working in close collaboration with those who do.
There are both direct and indirect paths to impact for the work in this thesis. Directly, the methodological contributions of Chapters 4 and 6 may eventually lead to marginally more accurate indicator estimates, contributing to a broadly more effective response. However, these improvements in accuracy seem of minor consequence within the broader context of the HIV response, and factors limiting its effectiveness. The applied contributions of Chapter 5 have a more promising case for direct impact. Indeed, I have seen evidence of engagement with this work by decision makers.
To the best of my abilities, this thesis, and the work described within it, was written in keeping with the principles of open science.
I hope that having done so facilitates my work to be scrutinised, and more optimistically, built upon.
In part this hope has already been realised, as with limited input from me, Dr. Kathryn Risher was able to extend my code for Chapter 5 to include additional countries (Panel 7.1B).
This would not have been possible without tools from the R ecosystem such as rmarkdown and rticles for reporting, devtools for R package development, as well as those written by software engineers within the MRC Centre for Global Infectious Disease Analysis such as orderly and didehpc.
It is crucial that academia adjusts to appropriately incentivise software contributions, and encourages adaption of open science best practices.
Work done to inform public health decision making should be held to high standards of transparency, reproducibility and collaboration.
Especially so in an outbreak response scenario (Grieve et al. 2023), where time is limited and decisions may be of significant consequence.